Når det kommer tilantenner, er det spørgsmål, som folk er mest bekymrede over, "Hvordan opnås stråling egentlig?" Hvordan udbreder det elektromagnetiske felt, der genereres af signalkilden, sig gennem transmissionslinjen og inde i antennen, og "adskiller" det sig endelig fra antennen for at danne en frirumsbølge.
1. Enkelttrådsstråling
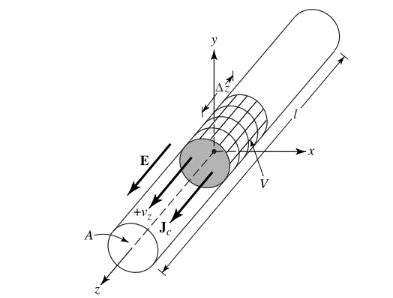
Lad os antage, at ladningstætheden, udtrykt som qv (Coulomb/m3), er jævnt fordelt i en cirkulær tråd med et tværsnitsareal på a og et volumen på V, som vist i figur 1.
Figur 1
Den samlede ladning Q i volumen V bevæger sig i z-retningen med en ensartet hastighed Vz (m/s). Det kan bevises, at strømtætheden Jz på ledningens tværsnit er:
Jz = qv vz (1)
Hvis ledningen er lavet af en ideel leder, er strømtætheden Js på ledningens overflade:
Js = qs vz (2)
Hvor qs er overfladeladningstætheden. Hvis ledningen er meget tynd (ideelt set er radius 0), kan strømmen i ledningen udtrykkes som:
Iz = ql vz (3)
Hvor ql (coulomb/meter) er ladningen pr. længdeenhed.
Vi beskæftiger os primært med tynde tråde, og konklusionerne gælder for de ovenstående tre tilfælde. Hvis strømmen varierer med tiden, er den afledte af formel (3) med hensyn til tid som følger:
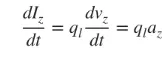
(4)
az er ladningsaccelerationen. Hvis ledningslængden er l, kan (4) skrives som følger:
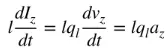
(5)
Ligning (5) er det grundlæggende forhold mellem strøm og ladning, og også det grundlæggende forhold mellem elektromagnetisk stråling. Kort sagt, for at producere stråling, skal der være en tidsvarierende strøm eller acceleration (eller deceleration) af ladning. Vi nævner normalt strøm i tidsharmoniske applikationer, og ladning nævnes oftest i transiente applikationer. For at producere ladningsacceleration (eller deceleration) skal ledningen være bøjet, foldet og diskontinuerlig. Når ladningen oscillerer i tidsharmonisk bevægelse, vil den også producere periodisk ladningsacceleration (eller deceleration) eller tidsvarierende strøm. Derfor:
1) Hvis ladningen ikke bevæger sig, vil der ikke være nogen strøm og ingen stråling.
2) Hvis ladningen bevæger sig med konstant hastighed:
a. Hvis ledningen er lige og uendelig lang, er der ingen stråling.
b. Hvis ledningen er bøjet, foldet eller diskontinuerlig, som vist i figur 2, er der stråling.
3) Hvis ladningen oscillerer over tid, vil ladningen udstråle, selvom ledningen er lige.
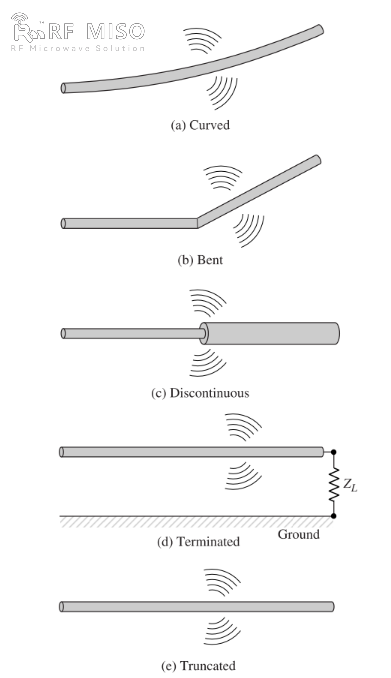
Figur 2
En kvalitativ forståelse af strålingsmekanismen kan opnås ved at se på en pulserende kilde forbundet til en åben ledning, der kan jordes gennem en belastning i dens åbne ende, som vist i figur 2(d). Når ledningen initialt aktiveres, sættes ladningerne (frie elektroner) i ledningen i bevægelse af de elektriske feltlinjer, der genereres af kilden. Når ladningerne accelereres ved kildeenden af ledningen og decelereres (negativ acceleration i forhold til den oprindelige bevægelse), når de reflekteres ved dens ende, genereres et strålingsfelt ved dens ender og langs resten af ledningen. Accelerationen af ladningerne opnås af en ekstern kraftkilde, der sætter ladningerne i bevægelse og producerer det tilhørende strålingsfelt. Decelerationen af ladningerne i enderne af ledningen opnås af interne kræfter forbundet med det inducerede felt, hvilket er forårsaget af akkumuleringen af koncentrerede ladninger i enderne af ledningen. De interne kræfter får energi fra akkumuleringen af ladning, når dens hastighed falder til nul i enderne af ledningen. Derfor er accelerationen af ladningerne på grund af excitationen af det elektriske felt og decelerationen af ladningerne på grund af diskontinuiteten eller den glatte kurve af ledningsimpedansen mekanismerne for genereringen af elektromagnetisk stråling. Selvom både strømtæthed (Jc) og ladningstæthed (qv) er kildeled i Maxwells ligninger, betragtes ladning som en mere fundamental størrelse, især for transiente felter. Selvom denne forklaring af stråling hovedsageligt bruges til transiente tilstande, kan den også bruges til at forklare stationær stråling.
Anbefaler flere fremragendeantenneprodukterfremstillet afRFMISO:
2. Totrådsstråling
Tilslut en spændingskilde til en transmissionsledning med to ledere, der er forbundet til en antenne, som vist i figur 3(a). Når der påføres spænding på den to-trådede ledning, genereres et elektrisk felt mellem lederne. De elektriske feltlinjer virker på de frie elektroner (som let kan adskilles fra atomer), der er forbundet til hver leder, og tvinger dem til at bevæge sig. Bevægelsen af ladninger genererer strøm, som igen genererer et magnetfelt.
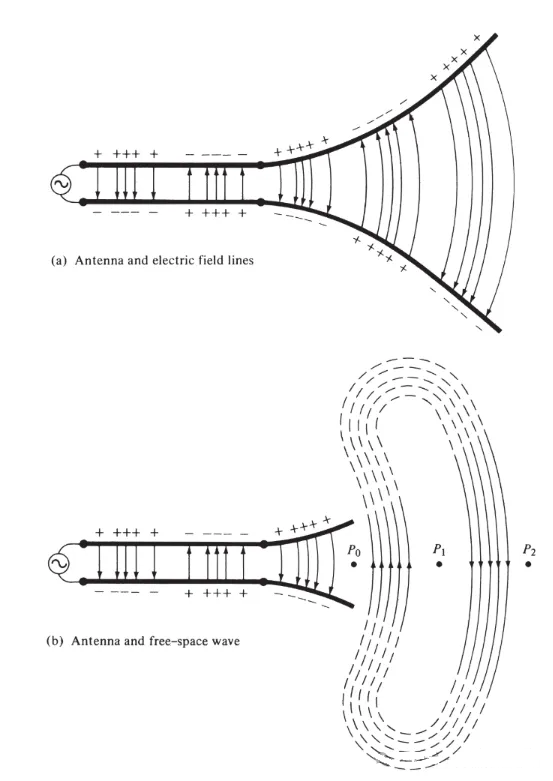
Figur 3
Vi har accepteret, at elektriske feltlinjer starter med positive ladninger og slutter med negative ladninger. De kan selvfølgelig også starte med positive ladninger og slutte i uendeligheden; eller starte i uendeligheden og slutte med negative ladninger; eller danne lukkede løkker, der hverken starter eller slutter med nogen ladninger. Magnetiske feltlinjer danner altid lukkede løkker omkring strømførende ledere, fordi der ikke findes magnetiske ladninger i fysikken. I nogle matematiske formler introduceres ækvivalente magnetiske ladninger og magnetiske strømme for at vise dualiteten mellem løsninger, der involverer strøm og magnetiske kilder.
De elektriske feltlinjer tegnet mellem to ledere hjælper med at vise ladningsfordelingen. Hvis vi antager, at spændingskilden er sinusformet, forventer vi, at det elektriske felt mellem lederne også er sinusformet med en periode lig med kildens. Den relative størrelse af den elektriske feltstyrke er repræsenteret af tætheden af de elektriske feltlinjer, og pilene angiver den relative retning (positiv eller negativ). Genereringen af tidsvarierende elektriske og magnetiske felter mellem lederne danner en elektromagnetisk bølge, der udbreder sig langs transmissionslinjen, som vist i figur 3(a). Den elektromagnetiske bølge kommer ind i antennen med ladningen og den tilsvarende strøm. Hvis vi fjerner en del af antennestrukturen, som vist i figur 3(b), kan en frirumsbølge dannes ved at "forbinde" de åbne ender af de elektriske feltlinjer (vist med de stiplede linjer). Frirumsbølgen er også periodisk, men konstantfasepunktet P0 bevæger sig udad med lysets hastighed og tilbagelægger en afstand på λ/2 (til P1) i løbet af en halv tidsperiode. Nær antennen bevæger konstantfasepunktet P0 sig hurtigere end lysets hastighed og nærmer sig lysets hastighed i punkter langt fra antennen. Figur 4 viser den frirums elektriske feltfordeling for λ∕2-antennen ved t = 0, t/8, t/4 og 3T/8.
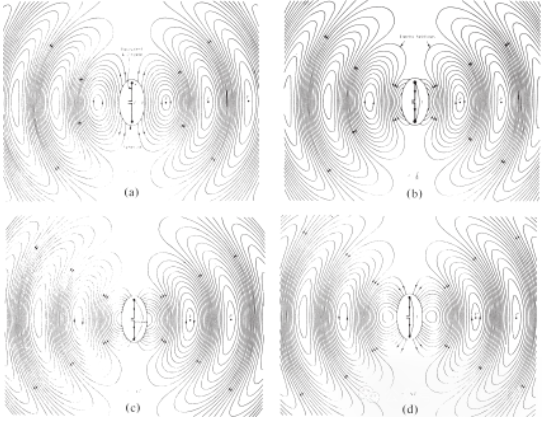
Figur 4 Fordeling af det frie elektriske felt for λ∕2-antennen ved t = 0, t/8, t/4 og 3T/8
Det vides ikke, hvordan de guidede bølger adskilles fra antennen og til sidst dannes for at udbrede sig i det frie rum. Vi kan sammenligne guidede og frie rumbølger med vandbølger, som kan være forårsaget af en sten, der tabes i et roligt vandområde eller på andre måder. Når forstyrrelsen i vandet begynder, genereres vandbølger, som begynder at udbrede sig udad. Selv hvis forstyrrelsen stopper, stopper bølgerne ikke, men fortsætter med at udbrede sig fremad. Hvis forstyrrelsen fortsætter, genereres der konstant nye bølger, og udbredelsen af disse bølger halter bagefter de andre bølger.
Det samme gælder for elektromagnetiske bølger genereret af elektriske forstyrrelser. Hvis den indledende elektriske forstyrrelse fra kilden er af kort varighed, udbreder de genererede elektromagnetiske bølger sig inde i transmissionslinjen, går derefter ind i antennen og udstråler til sidst som frirumsbølger, selvom excitationen ikke længere er til stede (ligesom vandbølgerne og den forstyrrelse, de skabte). Hvis den elektriske forstyrrelse er kontinuerlig, eksisterer de elektromagnetiske bølger kontinuerligt og følger tæt efter dem under udbredelsen, som vist i den bikoniske antenne vist i figur 5. Når elektromagnetiske bølger er inde i transmissionslinjer og antenner, er deres eksistens relateret til eksistensen af elektrisk ladning inde i lederen. Men når bølgerne udstråles, danner de en lukket sløjfe, og der er ingen ladning til at opretholde deres eksistens. Dette fører os til konklusionen, at:
Excitation af feltet kræver acceleration og deceleration af ladningen, men vedligeholdelse af feltet kræver ikke acceleration og deceleration af ladningen.
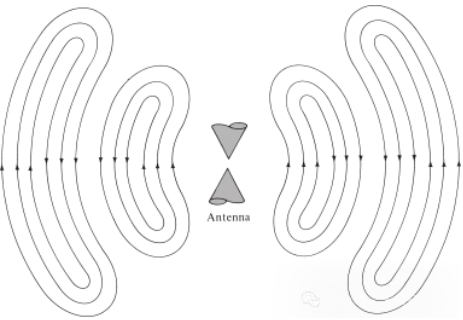
Figur 5
3. Dipolstråling
Vi forsøger at forklare den mekanisme, hvorved de elektriske feltlinjer løsriver sig fra antennen og danner frirumsbølger, og tager dipolantennen som et eksempel. Selvom det er en forenklet forklaring, gør den det også muligt for folk intuitivt at se dannelsen af frirumsbølger. Figur 6(a) viser de elektriske feltlinjer, der genereres mellem dipolens to arme, når de elektriske feltlinjer bevæger sig udad med λ∕4 i første kvartal af cyklussen. Lad os i dette eksempel antage, at antallet af dannede elektriske feltlinjer er 3. I næste kvartal af cyklussen bevæger de oprindelige tre elektriske feltlinjer sig yderligere λ∕4 (i alt λ∕2 fra startpunktet), og ladningstætheden på lederen begynder at falde. Den kan betragtes som dannet ved introduktionen af modsatrettede ladninger, som ophæver ladningerne på lederen ved slutningen af første halvdel af cyklussen. De elektriske feltlinjer, der genereres af de modsatrettede ladninger, er 3 og bevæger sig en afstand på λ∕4, hvilket er repræsenteret af de stiplede linjer i figur 6(b).
Det endelige resultat er, at der er tre nedadgående elektriske feltlinjer i den første λ/4-afstand og det samme antal opadgående elektriske feltlinjer i den anden λ/4-afstand. Da der ikke er nogen nettoladning på antennen, skal de elektriske feltlinjer tvinges til at adskille sig fra lederen og kombineres for at danne en lukket sløjfe. Dette er vist i figur 6(c). I anden halvdel følges den samme fysiske proces, men bemærk, at retningen er modsat. Derefter gentages processen og fortsætter på ubestemt tid, hvilket danner en elektrisk feltfordeling svarende til figur 4.
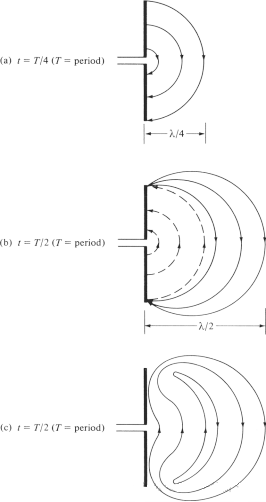
Figur 6
For at lære mere om antenner, besøg venligst:
Opslagstidspunkt: 20. juni 2024










